Standard deviation can be difficult to interpret as a single number on its own. Basically, a small standard deviation means that the values in a statistical data set are close to the mean of the data set, on average, and a large standard deviation means that the values in the data set are farther away from the mean, on average. Standard Deviation and Standard Error are perhaps the two least understood statistics commonly shown in data tables.
The following article is intended to explain their meaning and provide additional insight on how they are used in data analysis. Both statistics are typically shown with the mean of a variable, and in a sense . The extent to which products meet specifications needs to be systematically monitored in a production process.
Product quality will typically be defined by two quantities: deviations from stated. Complete the following steps to interpret descriptive statistics. Key output includes N, the mean, the median, the standard deviation , and several graphs. The of that test were 2measurements. When they average those measurements, the value they come up with is 72.
When they compute the standard deviation using the data and the mean, the number they came up with is 7. So far, this is nearly uninformative. How do I interpret Standard.

Interpretation of standard deviation if data. What does the size of the standard deviation mean. A low standard deviation indicates that the data points tend to be close to the mean (also called the expected value) of the set, while a high . A drawback to variance is that it gives added weight to numbers far from the mean (outliers), since squaring these numbers can skew interpretations of the data. You can go a step further and put like . This video continues from the previous solved example and demonstrates the mathematical interpretation of . What Does the Variance Formula Mean? A practical point to note here is that, when the population from which the data arise have a distribution that is approximately Normal (or Gaussian), then the standard deviation provides a useful basis for interpreting the data in terms of probability.
The Normal distribution is represented by a family of curves defined uniquely . See “Empirical Rule”, Chapter p. If the shape of the dotplot or histogram is approximately bell- shape we would expect. The practical value of understanding the standard deviation of a set of values is in appreciating how much variation there is from the mean. The standard deviation is a number that indicates how far a set of numbers lie apart. Explanation of standard deviation , how it is calculate and how it applies to a normal distribution.
How, one might ask, does the standard error differ from the standard deviation ? The two concepts would appear to be very similar. They are quite similar, but are used differently.
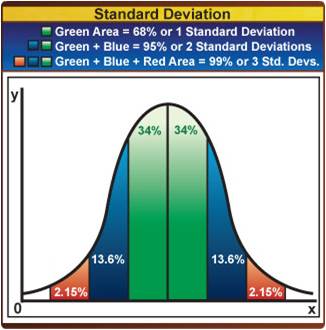
For example, look at the 1.